What is Programmable Vertex Pulling?

For years now vertex shaders have been supplied with Vertex data provided by the Input Assembler[1] following a fixed, user-specified layout. The vertices had to come from a specialized Vertex Buffer bound with a command dedicated to vertex buffers.

Programmable Vertex Pulling on the other hand is fully universal. Data is provided by a generic Storage Buffer bound via a descriptor set so you can read Vertex data just like you would read any other structured array. It allows for a more unified code that doesn’t handle vertices differently between shaders and commands.

It also comes with other benefits and some risks but that will be discussed throughout the whole blog post.

Programmable Vertex Pulling in Vulkan

It’s high time for a couple of changes in the graphics pipeline creation code, VkVertexInputBindingDescription and VkVertexInputAttributeDescription structures can both get deleted now. That’s because the VkPipelineVertexInputStateCreateInfo structure is meaningless if we don’t specify any input layouts and it can be left empty during pipeline creation:

VkPipelineVertexInputStateCreateInfo vertex_input_state{
    .sType = VK_STRUCTURE_TYPE_PIPELINE_VERTEX_INPUT_STATE_CREATE_INFO
};

Sadly it is not possible to completely remove it according to the specification[2].

Assuming you want to access the vertices in the Vertex Shader, add a new Storage Buffer binding, preferably with a scalar[3] block layout and read the array by indexing it with gl_VertexIndex:

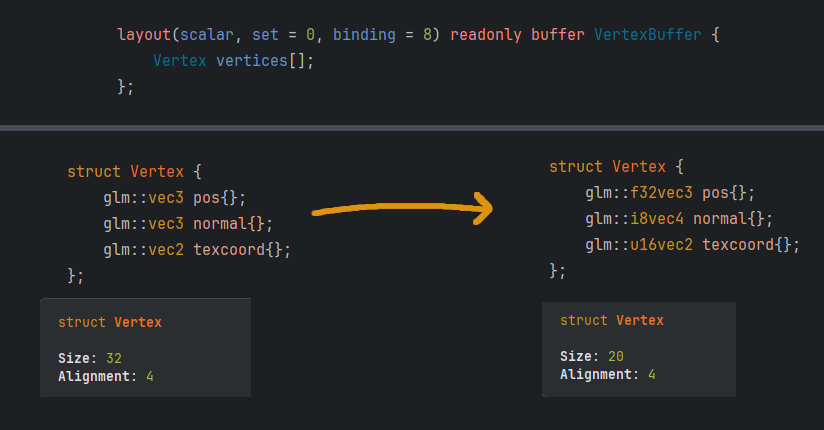
layout(scalar, set = ..., binding = ...) readonly buffer VertexBuffer {
    Vertex vertices[];
};

...

vec3 position = vertices[gl_VertexIndex].position;

Then during rendering bind a descriptor containing the Storage Buffer and that is basically what simple Programmable Vertex Fetching is all about :)

Scalar[3] block layout

It essentially makes the block behave like a C-style struct where each element is aligned to its internal scalar size. For vec3 it would be 4 bytes of alignment instead of the standard 16 bytes since the size of a float is exactly 4 bytes. This allows us to store tightly packed Vertex data in Storage Buffers. This also applies to 16-bit and 8-bit types.

This non-standard block layout was introduced in the GL_EXT_scalar_block_layout GLSL extension and VK_EXT_scalar_block_layout Vulkan 1.1 extension.

That’s why it has to enabled in GLSL with #extension GL_EXT_scalar_block_layout : require. Since the Vulkan extension was promoted to core Vulkan 1.2, we only need to enable the scalarBlockLayout physical device feature found in the VkPhysicalDeviceVulkan12Features structure.

8-bit and 16-bit types in GLSL

Switching to Programmable Vertex Pulling is a good moment to consider using lighter types like f16vec2 or i8vec4 in order to save quite a lot of memory. In my case I reduced the memory usage per-vertex by 38%. From 32 bytes per-vertex down to 20 bytes. That is a meaningful improvement especially that GPUs are often memory-bound.

By default GLSL won’t allow to store 16-bit or 8-bit types in a buffer but you can enable the full support with these two GLSL extensions:

#extension GL_EXT_shader_16bit_storage : require
#extension GL_EXT_shader_8bit_storage : require

Enabling those also requires enabling those four Vulkan physical device features:

VkPhysicalDeviceVulkan12Features features_vk_1_2 {
    .storageBuffer8BitAccess = true,
    .uniformAndStorageBuffer8BitAccess = true,
}

VkPhysicalDeviceVulkan11Features features_vk_1_1 {
    .storageBuffer16BitAccess = true,
    .uniformAndStorageBuffer16BitAccess = true,
}

Now with all of those fancy new types my Vertex structure looks like this:

struct Vertex {
    vec3 position;
    i8vec4 normal;
    f16vec2 texcoord;
};

And all that is left to do is actually pulling the vertex data and casting it to wider 32-bit types. Casting is rather neccessary because most of the shader code uses other 32-bit values:

vec3 v_position = vertices[gl_VertexIndex].position;
vec3 v_normal = vec3(ivec3(vertices[gl_VertexIndex].normal)) / 127.0f;
vec2 v_texcoord = vec2(vertices[gl_VertexIndex].texcoord);

I’ll explain how I pack normals and texture coordinates in later subsections.

Texture coordinates in f16vec2?

32-bit and 16-bit floating point formats differ quite a lot. Mostly in terms of how large or small of a number they can represent. The max representable value of 16-bit floats is only 65504 while the max value for 32-bit floats is about 3.4028235 * 10³⁸.

IEEE 754 single-precision binary floating-point format layout:

Source: [5]

IEEE 754 half-precision binary floating-point format layout:

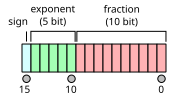
Source: [6]

In our case where we use f16vec2 only for texture coordinates we will mostly consider values that are between 0.0 and 1.0. According to Wikipedia[6], for such range 16-bit floats have a precision between 2^-14 and 2^-11 which is definitely enough. Therefore it is a viable option.

Here comes the magic trick - Converting 32-bit float to a 16-bit float and vice-versa. Here is a really quick and concise method of converting those types I found on Stack Overflow:

typedef unsigned short ushort;
typedef unsigned int uint;

uint as_uint(const float x) {
    return *(uint*)&x;
}
float as_float(const uint x) {
    return *(float*)&x;
}

float half_to_float(const ushort x) { // IEEE-754 16-bit floating-point format (without infinity): 1-5-10, exp-15, +-131008.0, +-6.1035156E-5, +-5.9604645E-8, 3.311 digits
    const uint e = (x&0x7C00)>>10; // exponent
    const uint m = (x&0x03FF)<<13; // mantissa
    const uint v = as_uint((float)m)>>23; // evil log2 bit hack to count leading zeros in denormalized format
    return as_float((x&0x8000)<<16 | (e!=0)*((e+112)<<23|m) | ((e==0)&(m!=0))*((v-37)<<23|((m<<(150-v))&0x007FE000))); // sign : normalized : denormalized
}
ushort float_to_half(const float x) { // IEEE-754 16-bit floating-point format (without infinity): 1-5-10, exp-15, +-131008.0, +-6.1035156E-5, +-5.9604645E-8, 3.311 digits
    const uint b = as_uint(x)+0x00001000; // round-to-nearest-even: add last bit after truncated mantissa
    const uint e = (b&0x7F800000)>>23; // exponent
    const uint m = b&0x007FFFFF; // mantissa; in line below: 0x007FF000 = 0x00800000-0x00001000 = decimal indicator flag - initial rounding
    return (b&0x80000000)>>16 | (e>112)*((((e-112)<<10)&0x7C00)|m>>13) | ((e<113)&(e>101))*((((0x007FF000+m)>>(125-e))+1)>>1) | (e>143)*0x7FFF; // sign : normalized : denormalized : saturate
}

Source: [4]

Using the code provided above it is trivially simple to convert 32-bit texture coordinates to 16-bit texture coordinates.

glm::u16vec2 packed_texcoord = glm::u16vec2(float_to_half(texcoord.x), float_to_half(texcoord.y));

Normals as i8vec4?

Let’s focus on normals since they suffered the most, reduced from 32-bits down to only 8-bits. It might seem like switching from 32-bit floating point data type down to just 8-bits would result in a catastrophically low precision for normals. Not only that, normals play a crucial role in lighting calculations which need rather precise directional data. But actually, normals have never needed high precision in the first place.

Since they are always normalized they only store a value between -1 and 1 for each component which is about 2 billion unique values[7] for a single component. Raise that value to the power of 3 for each of the xyz components and now 32-bits seem like an absolute overkill and a waste of memory.

8-bit signed integers can store values between -127 and 128 but a range of [-127, 127] will be perfect for normalized values since it’s symmetrical. Now with that knowledge we can easy tell that we can store up to 255³ unique vectors using just three 8-bit integers where 127 represents 1.0 and -127 represents -1.0. Because all of those vectors will be normalized - every single vector will be on the unit sphere - the actual value of possible directions represented will get much smaller but it will be still enough. Normal values are only per-vertex and per-fragment values will be interpolated anyways so you will not be able to tell the difference.

Now the conversion from 32-bit normal data to 8-bit is really straightforward thanks to the amazing GLM[8] math library:

glm::i8vec4 packed_normal = glm::i8vec4(glm::normalize(normals[i]) * 127.0f, 0.0f);

What about packed_normal.w? Well, now it’s just for padding but you can use the fourth component as additional space (32-bits in total) to pack the original XYZ values 10-bits per component which would increase the precision by a lot.

Now let’s see some actual data. I tested the precision of 8-bit integer normals by converting them back to 32-bit float vectors and calculating the dot product between them and the original normal values. Here’s how it turned out:

Average dot product (Raw): 0.994173
Max dot product (Raw): 0.999752
Min dot product (Raw): 0.988149

Average dot product (Normalized): 0.999997
Max dot product (Normalized): 1
Min dot product (Normalized): 0.999949

Average length difference: 0.00581642
Max length difference: 0.0118503
Min length difference: 0.000248015

… where for each vertex:

float dot_raw = glm::dot(normal, packed_normal_f32);
float dot_norm = glm::dot(normal, glm::normalize(packed_normal_f32));
float length_diff = glm::abs(glm::length(packed_normal_f32) - glm::length(normal));

The test mesh was the default Monkey mesh from Blender with the Subdivision Surface modifier and smooth shading applied to it:

The closer the dot product is to 1.0 the better. Both in terms of preserving the actual direction and length which should remain close to 1.0. Even if the length difference turned out to be higher than acceptable I could always normalize the values in shaders.

As you can see even the un-normalized 8-bit normals performed really well. In the worst-case scenario the dot product is equal to about 0.988. This means that in the worst-case scenario the normal would be off by about 9 degrees (α = arccos(0.988) * 180 / π ≈ 9°). If I normalized the values the error would be less than one degree.

Results

Performance

There has been no noticable difference in performance which is not really surprising. Vertex input bandwith in the main geometry pipeline was only a small fraction of the frametime and VRAM was far from being capped-out. (Tested on RTX 3070 Ti)

More memory-bound devices like iGPUs or mobile GPUs would most likely benefit from smaller vertices. Although there is a real risk that Programmable Vertex Pulling would cause performance impairments.

Memory usage

As mentioned before, I managed to cut down Vertex size from 32 bytes down to 20 bytes which is 38% smaller (62% of the original size). It means that I can store 60% more vertices in the same amout of memory:

If position precision was not a concern I could cut down Vertex size down to 14 bytes which would be 56% smaller (44% of the original size).

Further possibilities and concerns

Position, texcoord and normal attributes can be easily split to separate arrays in order to significantly speed up shaders which don’t rely on all three. Depth Prepass and Shadow Mapping would certainly benefit from having a position-only vertex array because the GPU would have only 12 bytes per-vertex to read instead of 20 bytes.

According to János Turánszki[9] Programmable Vertex Fetching could severly impair performance on older NVidia GPUs. Modern hardware shouldn’t be affected by it (except for iGPUs).

Bibliography

1. Graphics Pipeline Overview, [Vulkan Tutorial by A. Overvoorde]
2. VkGraphicsPipelineCreateInfo Specification, [The Khronos Group Inc.]
3. Scalar Block Layout, [The Khronos Group Inc.]
4. 32-bit to 16-bit Floating Point Conversion, [ProjectPhysX @ Stack Overflow 2020]
5. Single-precision floating-point format, [Wikipedia]
6. Half-precision floating-point format, [Wikipedia]
7. How many unique values are there between 0 and 1 of a standard float?, [Jeppe Stig Nielsen @ Stack Overflow 2013]
8. GLM Math Library, [g-truc]
9. Should we get rid of Vertex Buffers?, [János Turánszki, 2017]